Funzioni e proprietà si occupa delle funzioni reali di variabile reale. Classificazione tipologie ed esempi esplicativi per padroneggiare l’argomento in vista dello studio di funzioni.

DOMINIO (O campo di esistenza o insieme di definizione)
È l’insieme dei valori assunti dalla variabile indipendente (X) a cui corrisponde un valore definito della variabile dipendente (Y)
Es. per la funzione Y = 2X+1 Il CE è tutto l’asse reale.
Es. per la funzione Y = tgX Il CE è tutto l’asse reale escluso X= π/2 +kπ
o semplicemente non è definita per X= π/2 +kπ
CODOMINIO
È l’insieme dei valori assunti dalla variabile dipendente (Y) a cui corrisponde un valore definito della variabile indipendente (x)
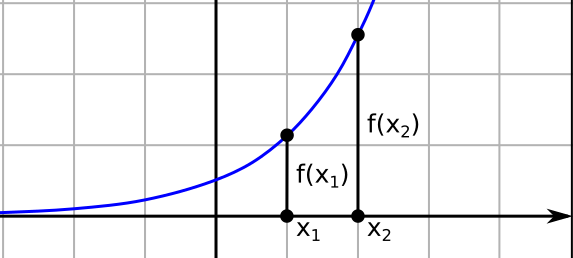
CRESCENTE
Una funzione si dice crescente in senso stretto, in un intervallo assegnato del dominio se risulta sempre f(x1) < f(x2) per x1 < x2
se risulta f(x1) ≤ f(x2) di dirà crescente in senso lato o non decrescente.
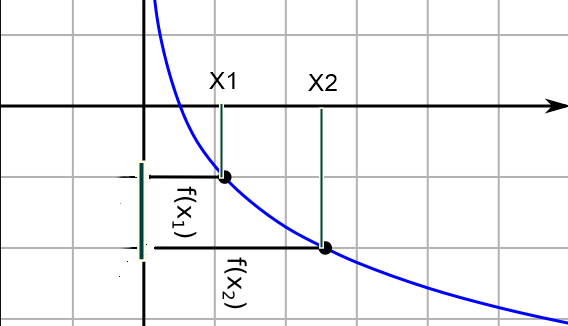
DECRESCENTE
Una funzione si dice decrescente in senso stretto, in un intervallo assegnato del dominio se risulta sempre f(x2) < f(x1) per x1 < x2
se risulta f(x2) ≤ f(x1 di dirà decrescente in senso lato o non crescente.
MONOTONA
una funzione si dice monotona in senso stretto se è sempre crescente o sempre decrescente.
FUNZIONI PERIODICHE
Una funzione si dice periodica, in un intervallo assegnato del dominio se risulta sempre f(x) = f(x+kT) con T periodo. Sono le ben note funzioni goniometriche.
FUNZIONI PARI
Una funzione si dice pari, in un intervallo assegnato del dominio se risulta sempre f(-x) = f(x)
Sono funzioni pari: la parabola con asse concidente con l’asse y; la funzione coseno; la funzione y=ІxІ
FUNZIONI DISPARI
Una funzione si dice dispari, in un intervallo assegnato del dominio se risulta sempre f(-x) = -f(x)
Sono funzioni dispari: le bisettrici Y=±x; la funzione seno;
La conoscenza delle funzioni e proprietà delle stesse è propedeutico per la prosecuzione dello studio della disciplina con particolare riferimento allo studio di funzioni.
