Le equazioni lineari sono delle uguaglianze tra due espressioni che può diventare una identità per particolari valori assunti dalle lettere.
L’uguaglianza è rappresentata dal simbolo = ad esempio a = 2b
Una identità è una uguaglianza verificata per qualsiasi valore attribuito alle lettere.
Quindi l’uguaglianza a = 2b diventa una identità solo se a risulta il doppio di b.
Una equazione è una uguaglianza che può diventare una identità per particolari valori attribuiti alla lettera.
Un esempio di equazione lineare è il seguente:
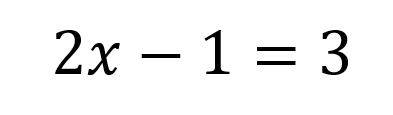
In questa espressione è possibile distinguere due parti separate dal simbolo di uguaglianza.
La parte che sta a sinistra si chiama 1° membro
La parte che sta a destra si chiama 2° membro
Questa uguaglianza può diventare una identità se x assume il valore 2.
Infatti 2*2 = 4 che diminuito di 1 fa 3.
L’equazione si dice lineare o di 1° grado quando la variabile è di 1° grado.
Il valore 2 che in questo caso rende l’uguaglianza una identità si chiama “soluzione dell’equazione” “radice dell’equazione” o “zero dell’equazione“.
Classificazione delle equazioni
un’equazione si dice intera se l’incognita figura solo al numeratore, in caso contrario si chiamerà fratta.
si dice numerica se i coefficienti sono solo numeri e non lettere, in caso contrario si chiamerà letterale.
In merito alle soluzioni le equazioni lineari saranno dette:
Determinate se esiste una sola soluzione
Indeterminate se esistono infinite soluzioni
Impossibili se non esistono soluzioni.
ESERCIZI
01 Esercizio equazioni lineari
